| Chemical Equations | Equations at the Atomic and Macroscopic Scale | Balancing Chemical Equations | |
| Mole Ratios | Predicting Mass Produced or Consumed in a Chemical Reaction | Limiting Reagents | |
- In Chemical Reactions Atoms Are What
- In Chemical Reactions Atoms Are Combined
- Which Best Describes A Chemical Reaction
- In Chemical Reactions Atoms Are *
Because atoms are neither created nor destroyed in a chemical reaction, the total mass of products in a reaction must be the same as the total mass of the reactants.
- Tell students that in a chemical reaction, the atoms in the reactants come apart, rearrange, and make new bonds to form the products. Represent the Chemical Equation. Have students use their remaining atoms to make the reactants again to represent the chemical reaction as a complete chemical equation.
- Unformatted text preview: Atoms in Chemical Reactions Glossary TERM DEFINITION chemical formula the symbolic representation of a substance subscript a small number at the lower right of a chemical symbol that shows the number of atoms molecule the smallest unit of a chemical element or compound that still has the chemical properties of that element or compound chemical bond an attractive force.
Chemical reactions are described by chemical equations.
In chemical reactions, atoms are neither created nor destroyed; they merely change partners. Thus the number of atoms of an element in the reaction’s products is equal to the number of atoms of that element in the original reactants. The coefficients we often place in front of one or more of the formulas in a chemical equation reflect this fact.
Example: The reaction between hydrogen and oxygen to form water is represented by the following equation.
2 H2 + O2 2 H2O
It is often useful to indicate whether the reactants or products are solids, liquids, or gases by writing an s, l, or g in parentheses after the symbol for the reactants or products, as shown in the following equations.
2 H2(g) + O2(g) 2 H2O(g)
2 Al(s) + Fe2O3(s) Al2O3(s) + 2 Fe(l)
Because so many reactions occur when solutions of two substances dissolved in water are mixed, a special symbol, aq, is used to describe these aqueous solutions.
The process in which a sample dissolves in water will be indicated by equations such as the following.
A chemical equation is a statement of what can happen, not necessarily what will happen. The following equation, for example, does not guarantee that hydrogen will react with oxygen to form water.
2 H2(g) + O2(g) 2 H2O(g)
It is possible to fill a balloon with a mixture of hydrogen and oxygen and find that no reaction occurs until you touch the balloon with a flame. The balanced equation for this reaction describes the relationship between the amounts of hydrogen and oxygen consumed and the water formed if or when this reaction is initiated.
Chemical equations can be used to represent what happens on either the atomic or macroscopic scale.
2 H2(g) + O2(g) 2 H2O(g)
This equation can be read in either of the following ways.
- If, or when, hydrogen reacts with oxygen, two molecules of hydrogen and one molecule of oxygen are consumed for every two molecules of water produced.
- If, or when, hydrogen reacts with oxygen, two moles of hydrogen and one mole of oxygen are consumed for every two moles of water produced.
Chemical equations must be balanced -- they must have the same number of atoms of each element on both sides of the equation. As a result, the mass of the reactants must be equal to the mass of the products of the reaction. On the atomic scale, the following equation is balanced because the total mass of the reactants is equal to the mass of the products.
| 2 H2(g) | + | O2(g) | 2 H2O(g) |
| 2 x 2 amu | + | 32 amu | 2 x 18 amu |
| 36 amu | 36 amu |
On the macroscopic scale, it is balanced because the mass of two moles of hydrogen and one mole of oxygen is equal to the mass of two moles of water.
| 2 H2(g) | + | O2(g) | 2 H2O(g) |
| 2 x 2 g | + | 32 g | 2 x 18 g |
| 36 g | 36 g |
There is no sequence of rules that can be followed blindly to get a balanced chemical equation. Manipulate the coefficients written in front of the formulas of the reactants and products until the number of atoms of each element on both sides of the equation are the same.
In Chemical Reactions Atoms Are What
.jpg)
| Interactive tutorial on balancing equations from requires Macromedia Shockwave |
It is usually a good idea to tackle the easiest part of a problem first.
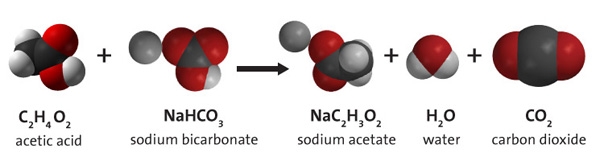
Example: Consider what happens when propane (C3H8) burns in air to form CO2 and H2O. The first thing to look for when balancing equations are relationships between the two sides of an equation.
_____ C3H8 + _____ O2 _____ CO2 + _____ H2O
It is easier to balance the carbon and hydrogen atoms in the equation than the oxygen atoms in this reaction because all of the carbon atoms in propane end up in CO2 and all of the hydrogen atoms end up in H2O, but some of the oxygen atoms end up in each compound. This means that there is no way to predict the number of O2 molecules that are consumed in this reaction until you know how many CO2 and H2O molecules are produced.
We can start by noting that there are three carbon atoms in each C3H8 molecule. Thus, three CO2 molecules are formed for every C3H8 molecule consumed.
1 C3H8 + _____ O2 3 CO2 + _____ H2O
If there are eight hydrogen atoms in each C3H8 molecule, there must be eight hydrogen atoms, or four H2O molecules, on the right side of the equation.
1 C3H8 + _____ O2 3 CO2 + 4 H2O
Now that the carbon and hydrogen atoms are balanced, we can try to balance the oxygen atoms. There are six oxygen atoms in three CO2 molecules and four oxygen atoms in four H2O molecules. To balance the 10 oxygen atoms in the products of this reaction we need five O2 molecules among the reactants.
1 C3H8 + 5 O2 3 CO2 + 4 H2O
There are now three carbon atoms, eight hydrogen atoms, and 10 oxygen atoms on each side of the equation. The balanced equation for this reaction is therefore written as follows.
C3H8(g) + 5 O2(g) 3 CO2(g) + 4 H2O(g)
| Practice Problem 6: Write a balanced equation for the reaction that occurs when ammonia burns in air to form nitrogen oxide and water. _____ NH3 + _____ O2 _____ NO + _____ H2O |
A balanced chemical equation allows us to predict what happens when the reaction takes place. A mole ratio converts moles of one compound in a balanced chemical equation into moles of another compound.
Example: The fireworks that brighten the sky each Fourth of July are based on the reaction between magnesium and oxygen to form magnesium oxide.
2 Mg(s) + O2(g) 2 MgO(s)
The balanced equation for this reaction can be used to construct two unit factors that describe the relationship between the amount of magnesium and oxygen consumed in this reaction.
By focusing on the units of this problem, we can select the correct mole ratio to convert moles of magnesium into an equivalent number of moles of oxygen. Assume, for example, that we want to calculate the number of moles of oxygen needed to burn 0.40 moles of magnesium metal.
| Practice Problem 7: A can of butane lighter fluid contains 1.20 moles of butane (C4H10). Calculate the number of moles of carbon dioxide given off when this butane is burned. |
Predicting the Mass of Reactants Consumed or Products Given Off in a Chemical Reaction
Balanced chemical equations can be used to predict the relationship between the amounts of the reactants consumed and the amounts of the products formed in a chemical reaction.
Example: To predict the amount of oxygen that must be inhaled to digest 10.0 grams of sugar we can assume that the sugar in our diet comes to us as C12H22O11 molecules and that our bodies burn this sugar according to the following equation.
C12H22O11(s) + 12 O2(g) 12 CO2(g) + 11 H2O(l)
Perhaps the best way to start is to ask: 'What are we trying to find?' and then summarize the important pieces of information in the problem.
Goal: Find out how many grams of O2 are consumed when 10.0 grams of sugar are burned.
Fact: We start with 10.0 grams of sugar.
Fact: Sugar has the formula C12H22O11.
Fact: The balanced equation for this reaction can be written as follows.
C12H22O11 + 12 O2 12 CO2 + 11 H2O
Because we know the molecular weight of sugar, we can convert the known mass of the sugar into the number of moles of sugar.
We now have a balanced chemical equation, and we know the number of moles of sugar in the sample. As a step toward the goal of the problem we might calculate the number of moles of oxygen consumed in the reaction. The equation for this reaction suggests that 12 moles of O2 are consumed for every mole of sugar in this reaction. We can therefore calculate the number of moles of oxygen needed to burn 0.02921 moles of sugar as follows.
We now have the necessary information to get to the goal of our calculation. We know the amount of O2 consumed in this reaction in units of moles and we can calculate the mass of 0.3505 moles of O2 from the molecular weight of oxygen.
According to this calculation, it takes 11.2 grams of O2 to burn 10.0 grams of sugar.
In Chemical Reactions Atoms Are Combined
| Practice Problem 8: Calculate the amount of ammonia and oxygen needed to prepare 3.00 grams of nitrogen oxide by the following reaction. 4 NH3(g) + 5 O2(g)4 NO(g) + 6 H2O(g) |
It takes 1.70 grams of ammonia and 4.00 grams of oxygen to make 3.00 grams of nitrogen oxide by the following reaction.
4 NH3(g) + 5 O2(g) 4 NO(g) + 6 H2O(g)
What would happen to the amount of NO produced in this reaction if we kept the amount of O2 the same (4.00 g) but increases the amount of NH3 that was present initially? The yield of the reaction would stay the same. No matter how much NH3 we add to the system, no more NO is produced because the reaction runs out of O2 before all of the NH3 is consumed. When this happens, the reaction must stop. No matter how much NH3 is added to the system, we can't get more than 3.00 grams of NO from 4.00 grams of oxygen.
When there isn't enough O2 to consume all the NH3 in the reaction, the amount of O2 limits the amount of NO that can be produced. Oxygen is therefore the limiting reagent in this reaction. Because there is more NH3 than we need, it is the excess reagent.
The concept of limiting reagent is important because chemists frequently run reactions in which only a limited amount of one of the reactants is present.
The key to limiting reagent problems is the following sequence of steps.
|
|
|
|
|
|
| Practice Problem 9: How much magnesium oxide (MgO) can be formed when 10.0 grams of magnesium reacts with 10.0 grams of O2? |
The atomic theory, first proposed in modern form by John Dalton, is one of the most important and useful ideas in chemistry. It interprets observations of the every-day world in terms of particles called atoms and molecules. Macroscopic events—those which humans can observe or experience with their unaided senses—are interpreted by means of microscopic objects—those so small that a special instrument or apparatus must be used to detect them. (Perhaps the term submicroscopic really ought to be used, because most atoms and molecules are much too small to be seen even under a microscope.) In any event, chemists continually try to explain the macroscopic world in microscopic terms.
To get a sense for just how small the atoms we will be working with in the next chapter are, check out this Ted-Ed video called 'Just How Small is an Atom'.
- 2.1: Prelude to Atoms and Reactions
- The atomic theory, first proposed in modern form by John Dalton, is one of the most important and useful ideas in chemistry. It interprets observations of the every-day world in terms of particles called atoms and molecules. Macroscopic events—those which humans can observe or experience with their unaided senses—are interpreted by means of microscopic objects—those so small that a special instrument or apparatus must be used to detect them.
- 2.2: Macroscopic Properties and Microscopic Models
- As a simple example of how the macroscopic properties of a substance can be explained on a microscopic level, consider the liquid mercury. Macroscopically, mercury at ordinary temperatures is a silvery liquid which can be poured much like water—rather unusual for a metal. Mercury is also the heaviest known liquid. Its density is 13.6 -fold greater than water. When cooled below –38.9°C mercury solidifies and behaves very much like more familiar solid metals such as copper and iron.
- 2.3: The Atomic Theory
- 2.4: Macroscopic and Microscopic Views of a Chemical Reaction
- 2.5: Testing the Atomic Theory
- To test a theory, we first use it to make a prediction about the macroscopic world. If the prediction agrees with existing data, the theory passes the test. If it does not, the theory must be discarded or modified. If data are not available, then more research must be done. Eventually the results of new experiments can be compared with the predictions of the theory.
- 2.6: Atomic Weights
- The relative masses of the atoms are usually referred to as atomic weights. The atomic-weight scale was originally based on a relative mass of 1 for hydrogen. As more accurate methods for determining atomic weight were devised, it proved convenient to shift to oxygen and then carbon, but the scale was adjusted so that hydrogen’s relative mass remained close to 1. Thus nitrogen’s atomic weight of 14.0067 tells us that a nitrogen atom has about 14 times the mass of a hydrogen atom.
- 2.7: The Amount of Substance- Moles
- 'How much?' in the above sense of the quantity of atoms or molecules present is not the same thing as 'how much' in terms of volume or mass. The International System of Measurements (IUPAC) has a measure of amount that reflects the number of atoms present, and it is called the mole.
- 2.8: The Mole
- The very large numbers involved in counting microscopic particles are inconvenient to think about or to write down. Therefore chemists have chosen to count atoms and molecules using a unit called the mole. One mole (abbreviated mol) is (6.022 times 10^{23}) of the microscopic particles which make up the substance in question.
- 2.9: The Amount of Substance
- In the International System this quantity is called the amount of substance and is given the symbol n.
- 2.10: The Avogadro Constant
- To obtain such a pure number, we need a conversion factor which involves the number of particles per unit amount of substance. The appropriate factor is given the symbol (N_A) and is called the Avogadro constant.
- 2.11: The Molar Mass
- It is often convenient to express physical quantities per unit amount of substance (per mole), because in this way equal numbers of atoms or molecules are being compared. Such molar quantities often tell us something about the atoms or molecules themselves.
- 2.12: Formulas and Composition
- When a reaction is carried out for the first time, little is known about the microscopic nature of the products. It is therefore necessary to determine experimentally the composition and formula of a newly synthesized substance. One way to approach this involves quantitative analysis—the determination of the percentage by mass of each element in the compound. Such data are usually reported as the percent composition.
- 2.13: Balancing Chemical Equations
Contributors
Which Best Describes A Chemical Reaction
Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.
In Chemical Reactions Atoms Are *
Thumbnail: Spinning Buckminsterfullerene ((ce{C60})). (CC BY-SA 3.0; unported; Sponk).
